Muons in Chemistry: Unique Studies of Quantum Mass Effects
Background Perspective
Atomic mass, and particularly the masses of different isotopes, has played an important role in both the physical and biological sciences since the discovery of deuterium by Harold Urey in 1932. Both mass and size matter and as we approach the nm and sub-nm sizes of atoms and nuclei, the observation of physical phenomena is dictated by the laws of quantum mechanics (QM). In the realm of isotopic mass, there are two key quantum mass effects: zero-point energy (ZPE) and tunneling through potential barriers. Both are manifestations of uncertainty in QM, embodied in the famous "Heisenberg Uncertainty Principle".
The Uncertainty Principle tells us that it is not possible to simultaneously determine position and momentum (or energy and time) with precision, so in the case of ZPE, a particle of mass 'm' must have motion even in its lowest energy state at zero Kelvin. Perhaps the most ubiquitous manifestation of this is in molecular spectroscopy, where the lowest-energy discrete vibrational states of the quantum oscillator exhibit features in analogy with simple harmonic motion. A simple everyday analog comes to mind - the rungs of a ladder. The lowest rung ('E0') does not sit on the ground, and the higher rungs could be thought of as the higher-lying vibrational states of a molecule with quantum numbers v=l, v=2 etc., though not equally spaced on a "quantum ladder".
Quantum tunneling really has no classical analog. It was discovered by George Gamov in 1928, who was puzzled by the fact that nuclear alpha decay was already quite well established by then, but how was the emitted α, with kinetic energies of typically ~ 6 MeV, able to scale the "Coulomb Barrier" of typically ~ 30 MeV? He reasoned that it had to "tunnel" through and derived an early result from wave mechanics for the probability of such barrier penetration. This result remains the central feature of tunneling processes today, now with widespread applications in science and engineering, including electron tunneling microscopy.
Isotopes are normally thought of as atoms with the same number of protons (same charge) but differing numbers of neutrons in their nucleus, and hence different atomic masses. The most sensitive effects of a change in mass, as outlined above, are found at the lightest end of the atomic mass scale, for the H atom. A dramatic example can be found in life processes: water is essential to life whereas "heavy water", D20, is toxic. Deuterium, due to its extra neutron, has twice the mass of H . Tritium (Rutherford, 1934), has two neutrons and hence three times the H atom mass, but is dangerously radioactive (can reside in the lungs) so has not seen widespread use in the chemical or biological sciences. How then to extend the atomic mass scale beyond the traditional factor of two brought to the table by deuterium? The answer is provided by muon science.
Isotopic Masses from Muon Science
Like electrons, muons come in two charge states, µ+ and µ-. They are naturally occurring on earth as components of cosmic rays, but are produced artificially at nuclear accelerators, like the TRIUMF cyclotron near UBC Chemistry. They are unstable with a mean life of 2.2 µs, in which either a positron (from µ+) or an electron (from µ-) and two neutrinos are emitted. Importantly, they have a mass only 1/9th the proton mass. The decay e+/e- is emitted preferentially along the muon spin, a consequence of the parity-violating nuclear weak interaction, providing the basis of the µSR technique that allows measurements of the interaction of the muon spin with its environment and notably here of chemical reactivity. There are two highly important muon 'isotopes' of the H atom, "muonium'' and "muonic helium''.
Muonium (Mu = µ+ e-) has a mass of only 0.114 amu, due to the mass of its µ+ ''nucleus'', on ~ 1/9th that of the proton, making it the lightest isotope of hydrogen. Though acting here as a light proton, the µ+ mass is still 200 times the electron mass, so Mu effectively has the same atomic size and ionization energy as H; i.e., the same "chemistry'', determined by the interactions of its outer electron.
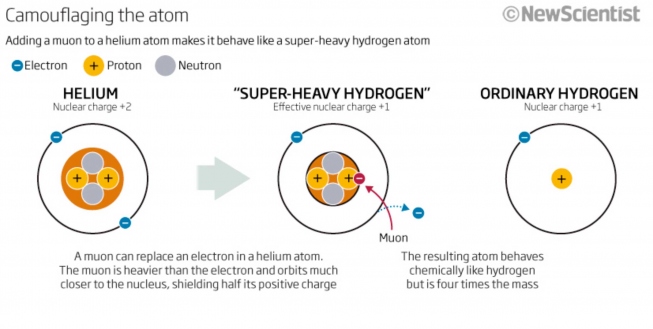
The heaviest isotope of H is formed by the capture of a µ- on 4He, into high-lying "muonic orbits'', which then rapidly cascades down to the muonic 1s state. Since the µ- mass is 200 times the electron mass, acting here as a heavy electron, it orbits 200 times closer to the helium nucleus, thereby negating one proton charge, camouflaging He and giving us "Super-Heavy Hydrogen'' (Heµ or, simply, 4H = [4Heµ-]+ e-), with a mass of 4.11 amu. This is schematically illustrated in Fig. 1 (New Scientist, 2011). Muonium would be just like `Ordinary Hydrogen' in this picture.
Chemical Reactivity of Mu and Heµ: Unique Tests of Quantum Mass Effects
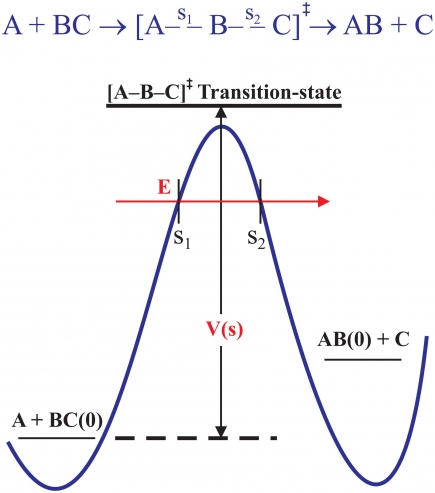
Many chemical reactions of interest are of the simple form A + BC → [A-B-C]‡ → AB +C, traversing the "transition state" (TS) [A-B-C]‡ between diatomic reactants and products. The overall electronic interaction potential energy along the path of the reaction is described by a "potential energy surface" (PES), a function of the distances between all three atoms. For the case of a collinear reaction, depicted in the schematic reaction path in Fig. 2, only two distances are needed. At both early and late times, at the limits of the reaction, the interactions in the 'BC' reactant (where s1 = RA-BC → -∞) and 'AB' product (where s2 = RC-BA → +∞) are attractive, "downhill" in energy; but at the TS on the reaction path, though not a real bound state, the close overlap of electrons causes a repulsive force that is "uphill" in energy and is manifest as a potential barrier, both energetics shown schematically by the solid blue curve in Fig. 2.
In any comparison of reaction rates between theory and experiment, knowing the (3D) PES is an essential first step. The most definitive comparisons are for the isotopic reaction rates of the 'H' + H2 reaction, and in particular here for Mu + H2 and Heµ + H2, providing for a remarkable range of a factor of 36 in isotopic mass and hence for uniquely sensitive tests of quantum mass effects in reaction rates, both the ZPE and quantum tunneling. The PES for the H + H2 reaction is still today (dating from ~ 1935), the only one known with the necessary accuracy ( ≤ 2 meV globally) to allow for truly definitive comparisons between experiment and truly rigorous quantum rate theory.
The total potential energy must also include ZPE along the complete reaction path. The ZPEs of the reactant, BC(0), and product, AB(0), are shown by the short horizontal black lines in Fig. 2, and by the longer thicker black line at the schematic level of the TS shown. This particular plot represents an endoergic reaction since the ZPE of the product AB(0) is shown as being greater than BC(0). The total barrier height, V(s) in the figure (labelled VS below), is determined by the difference in total energies between the TS and BC(0), not by the difference in electronic PE alone (blue curve). How fast or slow a reaction is depends directly on the height (and width) of VS, recognized phenomonologically much earlier, in 1869, by the Swedish chemist Svante Arrhenius, in terms of an experimentally determined "activation energy'', Ea, described by the famous Arrhenius equation, k(T) =à e-Ea/RT, for the T-dependence of the rate constant, where à is the collision rate between A and BC and 'R' is the "gas constant" (8.314 J mol-1 K-1).
Arrhenius's time predated quantum mechanics so the average energy 'E' of the reaction had to be high enough to exceed the barrier height VS for reaction to occur, dictating that the rates of many chemical reactions increase with increasing temperature (though not all, see below). In a quantum world, we also have to take account of tunneling through the barrier, as outlined earlier in the case of nuclear α decay. This is depicted by the red arrow in Fig. 2. The total energy of the system is the sum of kinetic and potential energies, E = Ekin + VS, a conserved quantity. Thus, classically, for reaction flux approaching from the left, when E = VS at the point s1 in this figure, Ekin → 0 at the "classical turning point'', and this flux would be reflected back without reaction. However, because of quantum tunneling, introduced above, this incident flux can pass through the barrier, emerging on the product side at s2 with the same E, though with reduced amplitude. It can be appreciated then that quantum tunneling will invariably give rise to a reduced activation energy compared to the magnitude of VS; it will also be manifest primarily at the lowest temperatures, where classical over-barrier reaction rate flux makes its smallest contribution to measured rate constants.
Every student of chemistry will have made an "Arrhenius plot'' of ln k(T) vs. 1/T at one time or another, expecting to see a straight-line dependence. However this is true only if Ea is T-independent, which is generally not the case except over a limited T range, as may be seen in the comparisons between experiment and rigorous quantum theory for the reaction rates of Mu and Heµ with H2 in the Arrhenius plot of Fig. 3. The colored points are the data, the colored lines the theory. The "thermal'' reaction rates (no state selection) for Mu +H2 (green) and Heµ + H2 (red) are contrasted with that for Mu + H2(v=1), where H2 has been state-selected in its first vibrational v=1 state (blue), the only result of its kind to date in Mu reactivity. These plots illustrate the features described above, as explained further below.
First consider the thermal Mu +H2 reaction (green points and theory line). This exhibits classic Arrhenius behaviour- a straight line dependence, giving a measured activation energy Ea = 0.58 eV (13.4 kcal/mol). The barrier to this reaction, being highly endoergic, is not only high, due to large contributions from ZPE shifts at the TS (see Fig. 2), but also wide, so that the probability of tunneling is very low in the T-range (~ 500 - 850 K), even for the light Mu atom. Contrast this result with that for the v=1 reaction (upper blue point and theory line). Note the curvature in this Arrhnenius plot, which is largely due to quantum tunneling, as outlined earlier, manifest at low temperatures and already evident at the 300 K point shown. Moreover, the excitation energy of H2(v=1) lies at 0.52 eV, so, simplistically, we could expect an activation energy in the region of the 300 K point of ~ 0.06 eV, also in accord with a major contribution from tunneling to this reaction, and entirely consistent with the slope of the theoretical line here. Experiments to measure the temperature dependence of this reaction rate are planned for the Spring of 2016.

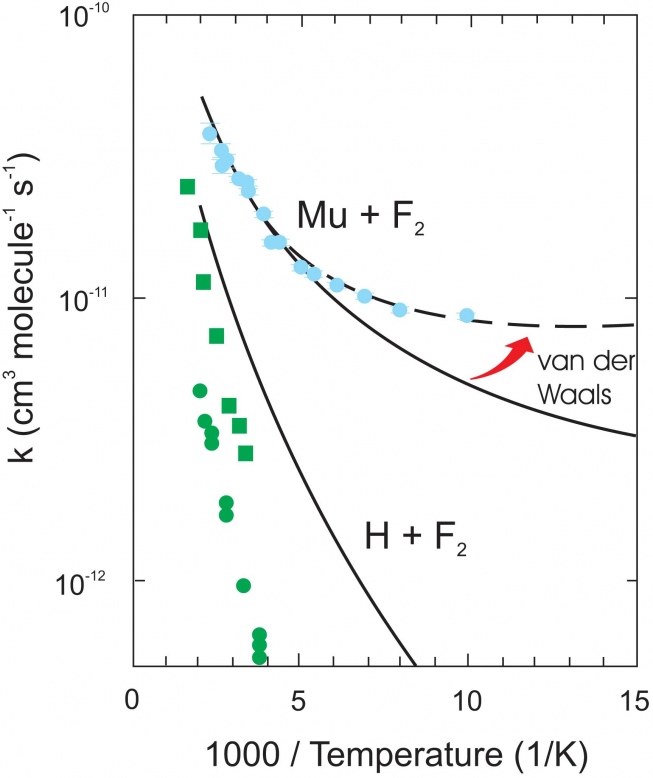
Returning now to the Arrhenius plots in Fig. 3, compare the results for the thermal rates of Mu + H2 (green line) and Heµ + H2 (red line). It can be seen that there is even a hint of curvature due to quantum tunneling at the lower Ts for the Heµ reaction, despite its much heavier mass (4.11 amu) compared to Mu (0.114 amu). This is a prime example of the interplay between mass and energetics in the study of kinetic isotope effects. The Heµ + H2 reaction is slightly exoergic, and hence gives rise to both a much lower and thinner barrier compared to the highly endoergic Mu + H2 reaction, with accordingly activation energies Ea ~ 0.3 eV and 0.58 eV, respectively. Zero-point energy also plays an important role here. Due to its heavy mass, ZPE contributions to the total barrier height VS at the TS for the Heµ reaction are considerably lower than for Mu + H2, giving rise to a much faster rate.
The exemplary level of agreement seen between rigorous quantum rate theory and experiment for the H3 reaction system in Fig. 3, over a factor of 36 in atomic mass (green and red lines) and 7 orders of magnitude in rate constants (green and blue lines) is, in a word, remarkable! Reaction dynamics in this system can now be regarded as a "solved problem'', one of only very few such examples in molecular quantum mechanics, thanks in part to muon science!
"Vibrational Bonding'' in BrMuBr: a new type of chemical bond
The existence of bound-state vibrations in potential wells, exemplified by the schematically shown in Fig. 2 state-selected v = 1 state of H2 in Fig.~3, has been a corner stone of molecular spectroscopy for a century. In rudimentary quantum chemistry calculations carried out on semi-empirical potential surfaces in the 1980s, the possibility of a new type of chemical bond, a ''vibrationally-bonded'' state that could be stabilized at the potential maximum of the TS or ''saddle point'' of the reaction in systems like IHI and BrHBr, was put forward. However, despite early reports for their observation, until recent studies from the realm of muon science, there had not been any definitive evidence for the existence of such vibrationally-bound states. These early quantum chemistry calculations did establish an important point though - in contrast to conventional molecular vibrations, the most stable vibrationally-bonded states correspond to the lightest atoms, and hence Mu, given the huge ZPE shift expected from Mu-bond formation, should be the ideal candidate for their observation.
This was actually indicated in an early (1989) kinetics study at TRIUMF of the rate constant, kMu(T), for the Mu + Br2 reaction, which showed a decreasing rate with temperature and hence a negative activation energy, suggesting the formation of an intermediate free-radical complex, which was subsequently confirmed in a much later (2012) experiment elsewhere. However, in that experiment it could not be determined whether vibrationally-bonded BrMuBr or a van-der-Waals Mu···Br2 molecule was being formed. That could only be established by rigorous quantum chemistry calculations.
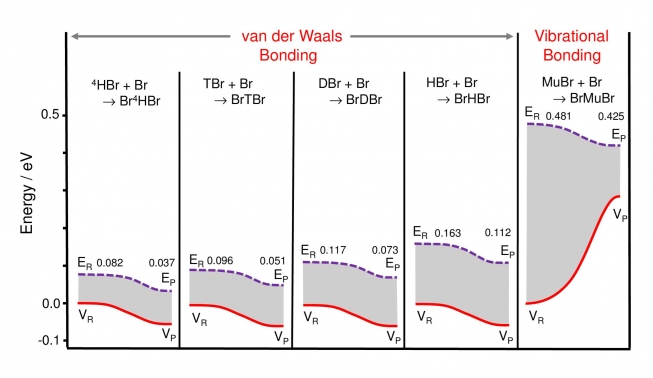
These followed soon after (2014) in a paper in Angewandte Chimie titled ''Fundamental Change in the Nature of Chemical Bonding by Isotopic Substitution''. This work established for the first time that BrMuBr is indeed stabilized at the TS of the potential, in a study of the symmetric Br + LBr → [BrLBr] → LBr + Br reaction, where 'L' represents the five possible isotopes of the H atom, from its heaviest, muonic He (4H), to its lightest, muonium (Mu). Only the Mu atom forms a stable vibrationally-bonded Br-Mu-Br system at the TS; all the heavier istopomers are stabilized in van-der-Waals wells, far removed from the barrier, as may be appreciated from the energetics shown in Fig. 5 below.
The values for the potential energy, VR and VP, and the total ground state energies (the sum of kinetic and potential energies) ER and EP, for the LBr + Br reactants and BrLBr products are shown. For all the heavy istopomers (4 panels on the left) both VP and EP for the products lie below those for for the reactants, consistent with conventional van der Waals bound states in potential wells with ''downhill'' energetics. In contrast, for vibrational bonding in BrMuBr (right panel), the potential energy show a dramatic increase (VP > VR), needed to overcome the potential barrier at the TS, but which is over-compensated by a marked decrease in ZPE at the saddle point (EP < ER) due to the very light muon mass. This reflects the well-known proportionality of ZPE to 1/√m, thereby providing a net gain in energy for this bound-state system, stabilized at the maximum of the potential surface.